Division of natural numbers.

Lesson 6

Division of Natural Numbers

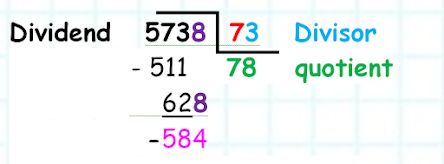
Objective: To know what division is and identify its parts.

Keywords: Division, dividend, divisor, quotient, remainder.

Vocabulary

Nº	English	Spanish

1	Close	Cerca/Cercano
2	Dividend	Dividendo
3	Divisor	Divisor
4	Look for	Buscar
5	Multiplication tables	Tablas de multiplicar
6	Quotient	Cociente
7	Remainder	Residuo
8	Share	Compartir
9	Split into	Dividir en
10	Solve	Resolver
11	Terms	Términos
12	Turn	Turno

Lesson Plan Nº6 - English version

Lesson Plan Nº6 - Spanish version

Let’s learn about:

The division is a method of distributing a group of things into equal parts. It is one of the four basic operations of arithmetic, which gives a fair result of sharing.

Remember:

The division is an operation inverse of multiplication

We use this symbol ÷, or sometimes / to make a division:

The division also has its part or terms. Pay attention to the following example: 22 divided by 5.

For making a division, it is important that you know the multiplication tables since they will help you solve a division.

Pay attention to this example:

There are 12 chocolates and 3 friends want to share them.

How do they divide the chocolate?

In this case, we take 12 chocolates, and we divide them by 3 friends.

Step Nº 1: Look for a number in the table of 3 that results in 12 or is close to this number.

In this case, 4 is the number because 3 x 4 = 12 and 4 will be the quotient

Step Nº 2: Multiply the Divisor (3) and the quotient (4)

Step Nº 3: Subtract twelve (12) and (12)

So, 12 ÷ 3 = 4 that means that each person must take 4 chocolates

Now, there is another example:

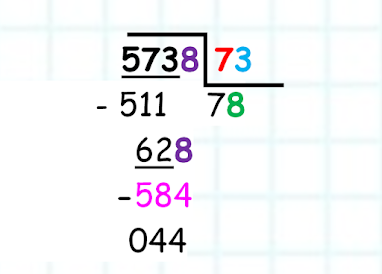
Step Nº 1: Take the first digits of the dividend: in this case 57. But as 57 is smaller than 73, you have to take one more digit: 573.

Step Nº 2: To divide 573 by 73, we take the first three digits of the dividend: 573 and divide them by the first digit of the divisor (7):

If we continue with the previous example, we would have to divide 57 by 7. Since 8 x 7 = 56, we will try 8.

We multiply 73 x 8 = 584 and since 584 is greater than 573, the 8 does not fit, so we would have to try with the previous number.

73 x 7 = 511 and since 511 is smaller than 573, the 7 if possible and we could do the subtraction of 573 - 511 = 62.

Step Nº 3: Lower the next digit and divide as in the previous step until there are no more digits.

Step Nº 4: Repeat the same procedure until there are no more digits.

We take again the first two digits 62 and we would have to divide them by 7. Since 8 x 7 = 56

We write 8 in the quotient and multiply 73 x 8 = 584. Since 584 is smaller than 628, we proceed to do the subtraction 628 - 584 = 44.

There are no more numbers to go down, we have finished the division! The result is 78 and the remainder is 44.

Types of Divisions

The above division might look easy but things get complicated as you move forward and that is why you should be aware of types of divisions. There are two types of division that you might encounter.

1. Exact Division

If you divide a number and the answer that you receive is zero that means it is an exact division. An exact division will always have the remainder zero (o).

2. Not Exact Division

If you divide a number but in the end, you still get a number that isn't divisible by the divisor that is the case of not exact division. The number which isn't divisible by the divisor is called the remainder. In simple words, a division is not exact when the remainder is not zero.